General Form of Back Propagation, Part 1
反向传播(Back Propagation, BP)是深度学习优化算法的核心,虽已有大量文章来介绍这个算法,但可惜往往都拘泥于某种具体模型,比如 Multilayer Perceptron,鲜有看到关于一般网络形式的讨论,中文资料更是如此。这样的坏处是经常陷入形式复杂的求导,而不容易理解 BP 的核心思想。所以我这里把之前针对一般形式的部分笔记整理出来,权作记录。
学界的一般共识认为,大脑的学习并不是通过梯度下降来完成的,G. Hinton 前些日子也表达了对反向传播的 “deeply suspicious”,但目前为止,反向传播依然是现今深度学习领域各模型的通用手段。
本文首先进行必要的形式化抽象,使得这里反向传播的讨论适用于一般网络模型;然后详细推导对于无环神经网络,反向传播如何进行;最后讨论如何将已有形式应用到有环的网络结构中,比如流行的 RNN/LSTM 等。
1. 问题形式化
1.1 网络拓扑抽象
命题:有向无环神经网络可以抽象为按层(layer)传播的单向链条,相邻层节点之间通过可微实函数连接。
显然这里我们省略了大量关于网络拓扑结构的严格定义和证明,但鉴于这只是一篇笔记就不写那么啰嗦了,熟悉基本神经网络概念的读者肯定知道上述命题想表达什么。
关于如何进行层结构的抽象,补充几点说明:
- 可根据需要进行必要的合并。因为我们关心的是如何更新模型参数,所以可将一些常见计算节点进行合并,比如全连接层和激活函数,这并不影响之后的讨论。
- 对于一些复杂结构,由有向无环的前提,可通过 BFS 之类算法得到满足前后依赖的偏序关系,进而抽象出需要的层结构。
- 如果有跨层使用的情况,比如 \(L + 1\) 层的计算同时使用了 \(L\) 层和 \(L - 1\) 层的节点,那么可以修改 \(L\) 层的计算函数,将 \(L - 1\) 层需要用到的节点利用单位函数「复制」一份到 \(L\) 层即可。因此后续讨论中,我们假定数据和计算依赖只存在于相邻层之间。
1.2 符号定义
我们这里使用最常见的随机梯度下降(SGD)来说明如何更新参数。设单次训练的样本对为 \((x, y)\),整体网络共有 \(L + 1\) 层,每一层的数据记作 \(a^{(l)}, l = 0,1,\dots,L\);第 0 层为输入,即 \(a^{0} = x\),最后一层输出为模型预测值,即 \(a^{L} = \hat{y}\)。层与层之间的计算函数设为 \(f^{(l)}\),对应模型参数为 \(\theta^{(l)}\)。为方便讨论,在 \(L\) 层后,我们添加损失函数计算,\(J = J(a^{(L)}, y)\)1。于是,我们得到如下前向传播计算公式:
\[ \begin{aligned} a^{(l)} & = f^{(l)}(a^{(l - 1)}, \theta^{(l)}), l = 1, \dots, L \\\ J & = J(a^{(L)}, y) \end{aligned} \]
需要仔细留意各层维度,设第 \(l\) 层数据维数为 \(n_l\),参数维度为 \(m_l\),即 \(a^{(l)}\in\mathbb{R}^{n_l}, \theta^{(l)}\in\mathbb{R}^{m_l}\),自然的 \(x\in\mathbb{R}^{n_0}, y\in\mathbb{R}^{n_L}\),对于损失函数则有 \(J\in\mathbb{R}\)。于是得到:
\[ \begin{aligned} f^{(l)}&: \mathbb{R}^{n_{l - 1} + m_l} \rightarrow \mathbb{R}^{n_l} \\\ J&: \mathbb{R}^{2n_{L}} \rightarrow \mathbb{R} \end{aligned} \]
2. 有向无环神经网络反向传播算法的一般形式
2.1 连接函数的 Jacobian 矩阵
由上述形式化定义,我们可以看到整个模型的参数全体是 \[\{\theta^{(l)}: l = 1,\dots,L\}\],而 SGD 的任务就是根据每步的训练数据,更新对应参数:
\[ \theta^{(l)} := \theta^{(l)} - \lambda\frac{\partial{J}}{\partial{\theta^{(l)}}} \]
为方便讨论,我们首先引入若干记号。
由 \(f^{(l)}(a^{(l - 1)}, \theta^{(l)})\) 可微,可分别计算其关于本层参数 \(\theta^{(l)}\) 与上一层输入数据 \(a^{(l - 1)}\) 的偏导(实际是 Jacobian 矩阵):
\[ \begin{aligned} P^{(l)} &:= \frac{\partial{f^{(l)}}}{\partial{\theta^{(l)}}} = \left( \frac{\partial{f^{(l)}_i}}{\partial{\theta^{(l)}_j}} \right)_{n_l\times m_l}, i = 1,\dots,n_l, j = 1,\dots,m_l \\\ Q^{(l)} &:= \frac{\partial{f^{(l)}}}{\partial{a^{(l-1)}}} = \left( \frac{\partial{f^{(l)}_i}}{\partial{a^{(l-1)}_j}} \right)_{n_l\times n_{l-1}}, i = 1,\dots,n_l, j = 1,\dots,n_{l-1} \end{aligned} \]
我们很快就会看到上述两个矩阵在反向传播中的核心作用。再次强调,\(P^{(l)}\) 和 \(Q^{(l)}\) 分别是 \(f^{(l)}\) 关于 \(\theta^{(l)}\) 和 \(a^{(l - 1)}\) 的 Jacobian 矩阵,尺寸分别为 \(n_l\times m_l\) 和 \(n_l\times n_{l-1}\)。
2.2 链式法则
我们按照从后向前的顺序更新所有模型参数 \(\theta^{(l)}\)。
最后第 \(L\) 层:
\[ \frac{\partial{J}}{\partial{\theta^{(L)}}} = \frac{\partial{J}}{\partial{a^{(L)}}} \cdot \frac{\partial{a^{(L)}}}{\partial{\theta^{(L)}}} \]
其中,由于 \(J = J(a^{(L)}, y)\) 形式已知,可以直接计算第一部分偏导,为方便,记
\[ \delta = \frac{\partial{J}}{\partial{a^{(L)}}} \in \mathbb{R}^{1\times n_L} \]
第二部分偏导则是上面已经计算过的 Jacobian 矩阵:
\[ \frac{\partial{a^{(L)}}}{\partial{\theta^{(L)}}} = \frac{\partial{f^{(L)}}}{\partial{\theta^{(L)}}} = P^{(L)} \in \mathbb{R}^{n_L\times m_L}\]
所以得到最后一层梯度更新结果为:
\[ \frac{\partial{J}}{\partial{\theta^{(L)}}} = \delta P^{(L)} \in\mathbb{R}^{1\times m_L}\]
中间层:
对于 \(\theta^{(l)}\) 而言,它只有通过其后各层的输出才能影响最后的 \(J\),因此简单利用链式法则,得到
\[ \begin{aligned} \frac{\partial{J}}{\partial{\theta^{(l)}}} & = \frac{\partial{J}}{\partial{a^{(L)}}} \cdot \frac{\partial{a^{(L)}}}{\partial{a^{(L-1)}}} \cdots \frac{\partial{a^{(l+1)}}}{\partial{a^{(l)}}} \cdot \frac{\partial{a^{(l)}}}{\partial{\theta^{(l)}}} \\\ & = \delta \cdot \frac{\partial{f^{(L)}}}{\partial{a^{(L-1)}}} \cdots \frac{\partial{f^{(l+1)}}}{\partial{a^{(l)}}} \cdot \frac{\partial{f^{(l)}}}{\partial{\theta^{(l)}}} \\\ & = \delta Q^{(L)}Q^{(L-1)}\cdots Q^{(l+1)}P^{(l)} \end{aligned} \]
类似的,我们可以验证上式最后矩阵相乘的各项维数,中间各个 \(Q^{(l)}\) 前后相接,维数依次「抵消」的过程会让人对所谓反向传播有新的体会。
2.3 小结前向后向传播算法
所以,现在我们可以从一个更宏观的层面来理解神经网络的前向与后向传播了。
核心就是 \(f^{(l)}\) 及其关于 parameter 与 input 的两个 Jacobian 矩阵 \(P^{(l)}, Q^{(l)}\)。前向传播时,由 \(a^{(l - 1)}\) 和 \(\theta^{l}\) 经由 \(f^{(l)}\) 得到 \(a^{(l)}\);后向传播时,注意到 \(a^{(L)}\) 事实上就是预测值 \(\hat{y}\),所以是从误差 \(J\) 关于 \(\hat{y}\) 的偏导 \(\delta\) 出发,从后向前,逐步经过 Jacobian 矩阵相乘得到梯度。
3. 循环神经网络的反向传播
以上讨论针对的神经网络计算图是所谓的有向无环图(DAG),对于常见的循环神经网络,从传统 RNN 到后来的 LSTM 以及各种变形,并不能直接套用。此时计算梯度下降往往采取的是所谓 Back Propagation Through Time (BPTT) 的方法。
简单说,就是对于输入序列在「时间维度」展开成一个普通无环图,于是又可以从后向前逐步计算梯度:
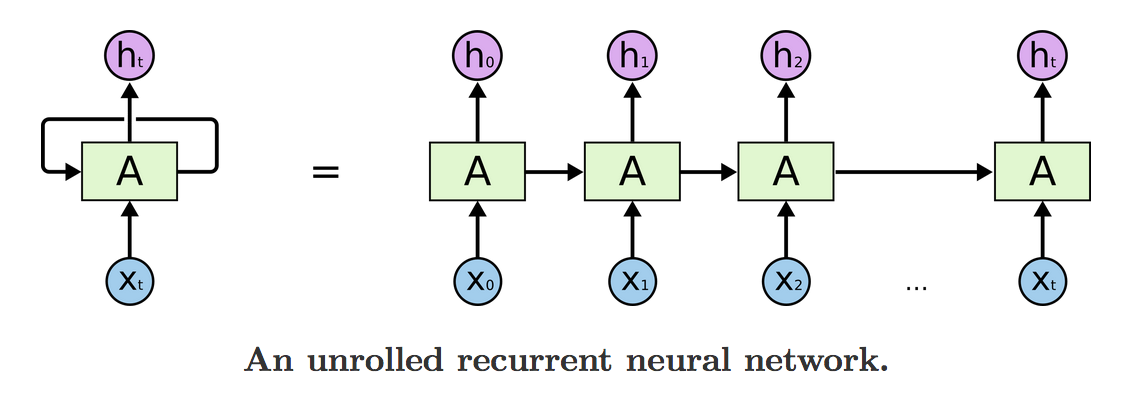
unrolled-rnn
(图片来自 colah’s blog)
关于 BPTT 的讨论可以参考 Denny Britz 和 Jason Brownlee 的这两篇文章。这里就不再详细展开了。
当然以上讨论主要是从理论层面给出神经网络反向传播算法的一般形式,这也是标题中用 “part 1” 的原因。实际工程中如何利用符号求导,特别是分布式环境下如何快速进行梯度更新,同样是很有意思的问题,容我继续研究一下再来写 part 2 吧:)
其实也可将最后 \(L\) 层直接看作损失函数的输出,推导是一样的,只不过需要将 label \(y\) 与输入 \(x\) 合并看作为新的输入。↩︎